Backtracking(Rat in Maze)

A Maze is given as N*N binary matrix of blocks where source block is the upper left most block i.e., maze[0][0] and destination block is lower rightmost block i.e., maze[N-1][N-1]. A rat starts from source and has to reach destination. The rat can move only in two directions: forward and down.

In the maze matrix, 0 means the block is dead end and 1 means the block can be used in the path from source to destination. Note that this is a simple version of the typical Maze problem. For example, a more complex version can be that the rat can move in 4 directions and a more complex version can be with limited number of moves.

Following is an example maze.

Gray blocks are dead ends(value = 0).

ratinmaze_filled

Following is binary matrix representation of the above maze

{1, 0, 0, 0}
{1, 1, 0, 1}
{0, 1, 0, 0}
{1, 1, 1, 1}

Following is maze with highlighted solution path.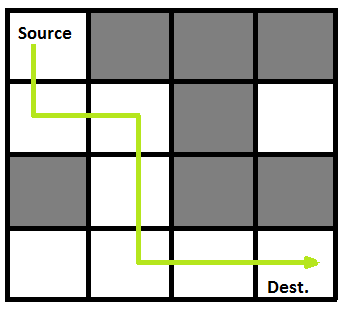

Following is the solution matrix(output of program) for the above input maze.

      {1, 0, 0, 0}
      {1, 1, 0, 0}
      {0, 1, 0, 0}
      {0, 1, 1, 1}
All entries in solution path are marked as 1.

Native Algorithm

The Naive Algorithm is to generate all paths from source to destination and one by one check if the generated path satisfies the constraints.

while there are untried paths
{
  generate the next path
  if this path has all blocks as 1
  {
    print this path;
  }
}

Backtracking Algorithm

If destination is reached
    print the solution matrix
Else
    a) Mark current cell in solution matrix as 1.
    b) Move forward in horizontal direction and recursively check if this
      move leads to a solution.
    c) If the move chosen in the above step doesn't lead to a solution
      then move down and check if  this move leads to a solution.
    d) If none of the above solutions work then unmark this cell as 0
      (BACKTRACK) and return false.

Implementation of Backtracking solution

/* C/C++ program to solve Rat in a Maze problem using
   backtracking */
#include<stdio.h>

// Maze size
#define N 4

bool solveMazeUtil(int maze[N][N], int x, int y, int sol[N][N]);

/* A utility function to print solution matrix sol[N][N] */
void printSolution(int sol[N][N])
{
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
            printf(" %d ", sol[i][j]);
        printf("\n");
    }
}

/* A utility function to check if x,y is valid index for N*N maze */
bool isSafe(int maze[N][N], int x, int y)
{
    // if (x,y outside maze) return false
    if(x >= 0 && x < N && y >= 0 && y < N && maze[x][y] == 1)
        return true;

    return false;
}

/* This function solves the Maze problem using Backtracking.  It mainly
   uses solveMazeUtil() to solve the problem. It returns false if no
   path is possible, otherwise return true and prints the path in the
   form of 1s. Please note that there may be more than one solutions,
   this function prints one of the feasible solutions.*/
bool solveMaze(int maze[N][N])
{
    int sol[N][N] = { {0, 0, 0, 0},
        {0, 0, 0, 0},
        {0, 0, 0, 0},
        {0, 0, 0, 0}
    };

    if(solveMazeUtil(maze, 0, 0, sol) == false)
    {
        printf("Solution doesn't exist");
        return false;
    }

    printSolution(sol);
    return true;
}

/* A recursive utility function to solve Maze problem */
bool solveMazeUtil(int maze[N][N], int x, int y, int sol[N][N])
{
    // if (x,y is goal) return true
    if(x == N-1 && y == N-1)
    {
        sol[x][y] = 1;
        return true;
    }

    // Check if maze[x][y] is valid
    if(isSafe(maze, x, y) == true)
    {
        // mark x,y as part of solution path
        sol[x][y] = 1;

        /* Move forward in x direction */
        if (solveMazeUtil(maze, x+1, y, sol) == true)
            return true;

        /* If moving in x direction doesn't give solution then
           Move down in y direction  */
        if (solveMazeUtil(maze, x, y+1, sol) == true)
            return true;

        /* If none of the above movements work then BACKTRACK:
            unmark x,y as part of solution path */
        sol[x][y] = 0;
        return false;
    }

    return false;
}

// driver program to test above function
int main()
{
    int maze[N][N]  =  { {1, 0, 0, 0},
        {1, 1, 0, 1},
        {0, 1, 0, 0},
        {1, 1, 1, 1}
    };

    solveMaze(maze);
    return 0;
}