algorithms
Divide and Conquer(Main Thoery)
if a>=1 and b > 1, T(n) = aT(n/b) + f(n)
case 1 \[ f(n) = O(n^{\log_b{a-\epsilon}}) \longrightarrow T(n) = \Theta(n^{\log_ba}) \]
- case 2 \[ f(n) = \Theta(n^{\log_ba}) \longrightarrow T(n) = \Theta(n^{\log_ba}\lg n) \]
case 3 \[ f(n) = \Omega(n^{\log_b{a+\epsilon}}) \longrightarrow T(n) = \Theta{f(n)}) \]
Fibonacci 数列近似值
\[ f(n) \approx 2^{0.694n} \approx (1.6)^{n} \]
对于排序数组的组合
可以做到\[O(n{\log_2{n}})\] Given a nonempty subset of indices S, define the children of S to be S {max(S)} U {max(S) + 1} and S U {max(S) + 1} 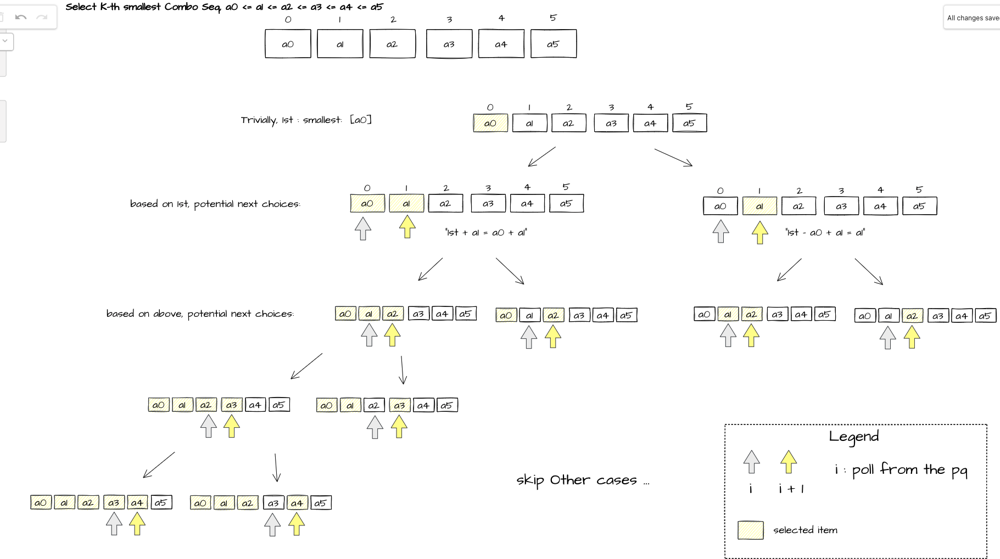

-------------本文结束感谢您的阅读-------------